excel圖表怎么將十進制數轉換成指定進制的數

excel圖表怎么將十進制數轉換成指定進制的數

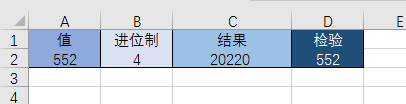
使用公式來解決問題：給定一個十進制的正整數，將其轉換成指定進制的數。如下所示，在單元格A2中是給定的十進制正整數值，單元格B2中是指定的進制，示例中是4進制，單元格C2中是轉換后的結果，單元格D2中使用公式檢驗結果是否正確。

在單元格C2中的公式是：

=SUMPRODUCT(MOD(FLOOR(A2/B2^(ROW(INDIRECT(“1:20”))-1),1),B2)*10^(ROW(INDIRECT(“1:20”))-1))

在單元格D2中的公式是：

=SUMPRODUCT(B2^(ROW(INDIRECT(“1:” &LEN(C2)))-1),0+MID(C2,1+LEN(C2)-ROW(INDIRECT(“1:” & LEN(C2))),1))

下面來詳細解釋公式是怎么得來的。

對于任何進制的數來說，其通用形式為：

其中，x代表進制數，a0、a1、a2、…、an是常量。

例如，對于我們熟悉的10進制來說，整數173可以表示為：

（1X100）+（7X10）+（3X1）

也可以寫作：

（1X10^2）+（7X10^1）+（3X10^0）

我們可以很容易地分解成這樣的表達式，但是我們如何指示Excel這樣做呢？我們可以給出什么指令，以便在給定諸如值173的情況下，可以生成一系列的返回值，即1、7和3分別對應于10^2、10^1和10^0的系數？我們所需要做的就是以某種方式找到一種將值173轉換為1個“百”，7個“十”和3個“一”的方法。

我們一般采用以下方式推導：

在173中有1個“百”。

減去1個“百”后，余下的73有7個“十”。

再減去7個“十”后，余下的3有1個“一”。

這些都是非常基本的東西。當然，我們可以在Excel中像上面一樣簡單地生成等效的算法過程。唯一的麻煩是，上述算法中的每一行都依賴于前一條。也就是說，我們要這樣進行設置：

如果嘗試將上所示工作表中的嘗試壓縮為一個公式可能有困難，因為列D中的每個公式都包含對其上一行的值的引用。

因此，沿著上述公式鏈條進行下去，如果我們希望使用一個公式從初始值173中獲得3，復合公式為：

=INT(D2-(INT(D2/10^2)*10^2)-(INT((D2-(INT(D2/10^2)*10^2))/10^1)*10^1)/10^0)

這顯然并不是我們想要的公式，太冗長了！如果要轉換為二進制的話，可想而知，公式會怎樣！

幸運的是，還有一種替代方法可以獲取每個值。仍以173為例，這次計算該值除以100、10和1中的每一個后取整得到的結果，然后將得到的結果除以基數10求余數：

這里，我們可以看到“結果”列中的值并不依賴于上面的每一行，這次可以使用下面簡單的公式得到3：

=MOD(INT($A$2/10^0),10)

沿著這個思路來構造上述方法的數組版本。我們唯一需要確定的事情是執行計算的數組大小，即在指定進制下所需要的最大指數是多少？

在上面的示例中，顯然需要的是“百”。因此，對于我們的10的指數需要由三個元素組：0、1和2組成的數組。如果考慮值10,301,444，那么顯然需要達到10^7，因此我們的數組將由8個元素組成（從10^0到10^7）。

實際上，這里決定采用一種比較“懶惰”的方法。不是動態確定此值，而是簡單地使用了一個較大的（至少以Excel術語來說）索引上限20。

當然，當我們使用除10以外的進制（基數）時，此過程也沒有什么不同。以本文開始時給出的示例為例，即將552轉換為4進制數，其部分公式為：

B2^(ROW(INDIRECT(“1:20”))-1)

得到一個由20個值組成的數組，該數組由4的0至19次方的結果組成：

{1;4;16;64;256;1024;4096;16384;65536;262144;1048576;4194304;16777216;67108864;268435456;1073741824;4294967296;17179869184;68719476736;274877906944}

然后被552除并向下取整：

FLOOR(A2/{1;4;16;64;256;1024;4096;16384;65536;262144;1048576;4194304;16777216;67108864;268435456;1073741824;4294967296;17179869184;68719476736;274877906944},1)

得到：

{552;138;34;8;2;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0}

接著，求除以4的余數：

MOD({552;138;34;8;2;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0},B2)

得到第一個數組：

{0;2;2;0;2;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0}

第二個數組更直接，由10的0至19次方的結果組成：

{1;10;100;1000;10000;100000;1000000;10000000;100000000;1000000000;10000000000;100000000000;1000000000000;10000000000000;100000000000000;1000000000000000;10000000000000000;100000000000000000;1000000000000000000;10000000000000000000}

因此，最后的結果為：

=SUMPRODUCT({0;2;2;0;2;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0}*{1;10;100;1000;10000;100000;1000000;10000000;100000000;1000000000;10000000000;100000000000;1000000000000;10000000000000;100000000000000;1000000000000000;10000000000000000;100000000000000000;1000000000000000000;10000000000000000000})

得到20220。

可以檢驗結果是否正確。如下：

(2X4^4)+(0X4^3)+(2X4^2)+(2X4^1)+(0X4^0)

等于：

(2X256)+(0X64)+(2X16)+(2X4)+(0X1)

等于：

512+0+32+8+0

結果為：

552。

版權聲明：本文內容由網絡用戶投稿，版權歸原作者所有，本站不擁有其著作權，亦不承擔相應法律責任。如果您發現本站中有涉嫌抄襲或描述失實的內容，請聯系我們jiasou666@gmail.com 處理，核實后本網站將在24小時內刪除侵權內容。

版權聲明：本文內容由網絡用戶投稿，版權歸原作者所有，本站不擁有其著作權，亦不承擔相應法律責任。如果您發現本站中有涉嫌抄襲或描述失實的內容，請聯系我們jiasou666@gmail.com 處理，核實后本網站將在24小時內刪除侵權內容。